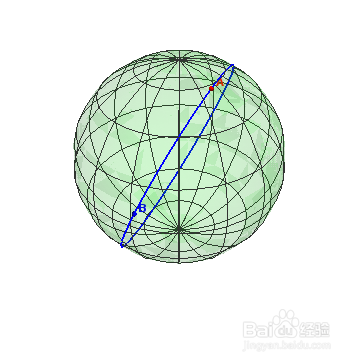
1、r[u_, v_] := {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]};a = Show[ParametricPlot3D[r[u,v],{u,0,2 Pi}, {v, 0, 2Pi},PlotStyle->Green],Axes->False,Boxed->False,PlotRange->All]

2、球面上的小圆一般不是测地线。

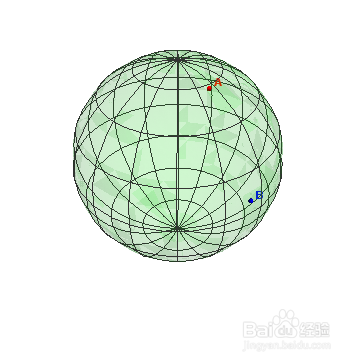
3、球面上A和B两个点:
a = Show[Graphics3D[{Red,Ball[r[2,3],0.02],Inset[Style["A",Red,Bold,10],r[2,3]+0.05],Blue,Ball[r[3,3],0.02],Inset[Style["B",Blue,Bold,10],r[3,3]+0.05]}],ParametricPlot3D[r[u,v],{u,0,2 Pi}, {v, 0, 2Pi},PlotStyle->{Green,Opacity[0.1]},ViewPoint->2r[2.5,2.36]],Axes->False,Boxed->False,PlotRange->All]
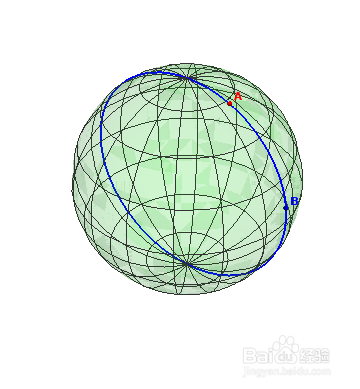
4、进过A、B的测地线是:
a = Show[Graphics3D[{Red,Ball[r[2,3],0.02],Inset[Style["A",Red,Bold,10],r[2,3]+0.05],Blue,Ball[r[3,3],0.02],Inset[Style["B",Blue,Bold,10],r[3,3]+0.05]}],ParametricPlot3D[r[u,3],{u,0,2 Pi},PlotStyle->{Blue}],ParametricPlot3D[r[u,v],{u,0,2 Pi}, {v, 0, 2Pi},PlotStyle->{Green,Opacity[0.1]},ViewPoint->2r[2.5,2.36]],Axes->False,Boxed->False,PlotRange->All]
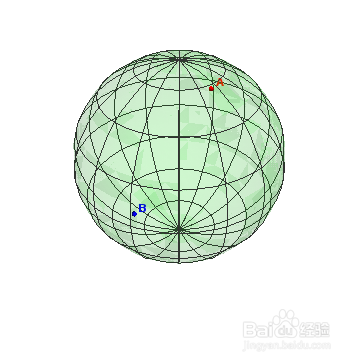
5、如果A和B不在同一条经线上:
a = Show[Graphics3D[{Red,Ball[r[2,3],0.02],Inset[Style["A",Red,Bold,10],r[2,3]+0.05],Blue,Ball[r[3,2],0.02],Inset[Style["B",Blue,Bold,10],r[3,2]+0.05]}],(*ParametricPlot3D[r[u,3],{u,0,2 Pi},PlotStyle->{Blue}],*)ParametricPlot3D[r[u,v],{u,0,2 Pi}, {v, 0, 2Pi},PlotStyle->{Green,Opacity[0.1]},ViewPoint->2r[2.5,2.36]],Axes->False,Boxed->False,PlotRange->All]
6、经过计算,可以得到这条测地线的参数方程:
h=RotationTransform[{{0,0,1}*1.,Cross[r[2,3],r[3,2]]*1.}][{Cos[u],Sin[u],0}]
a = Show[Graphics3D[{Red,Ball[r[2,3],0.02],Inset[Style["A",Red,Bold,10],r[2,3]+0.05],Blue,Ball[r[3,2],0.02],Inset[Style["B",Blue,Bold,10],r[3,2]+0.05]}],ParametricPlot3D[h,{u,0,2 Pi},PlotStyle->{Blue}],ParametricPlot3D[r[u,v],{u,0,2 Pi}, {v, 0, 2Pi},PlotStyle->{Green,Opacity[0.1]},ViewPoint->2r[2.5,2.36]],Axes->False,Boxed->False,PlotRange->All]