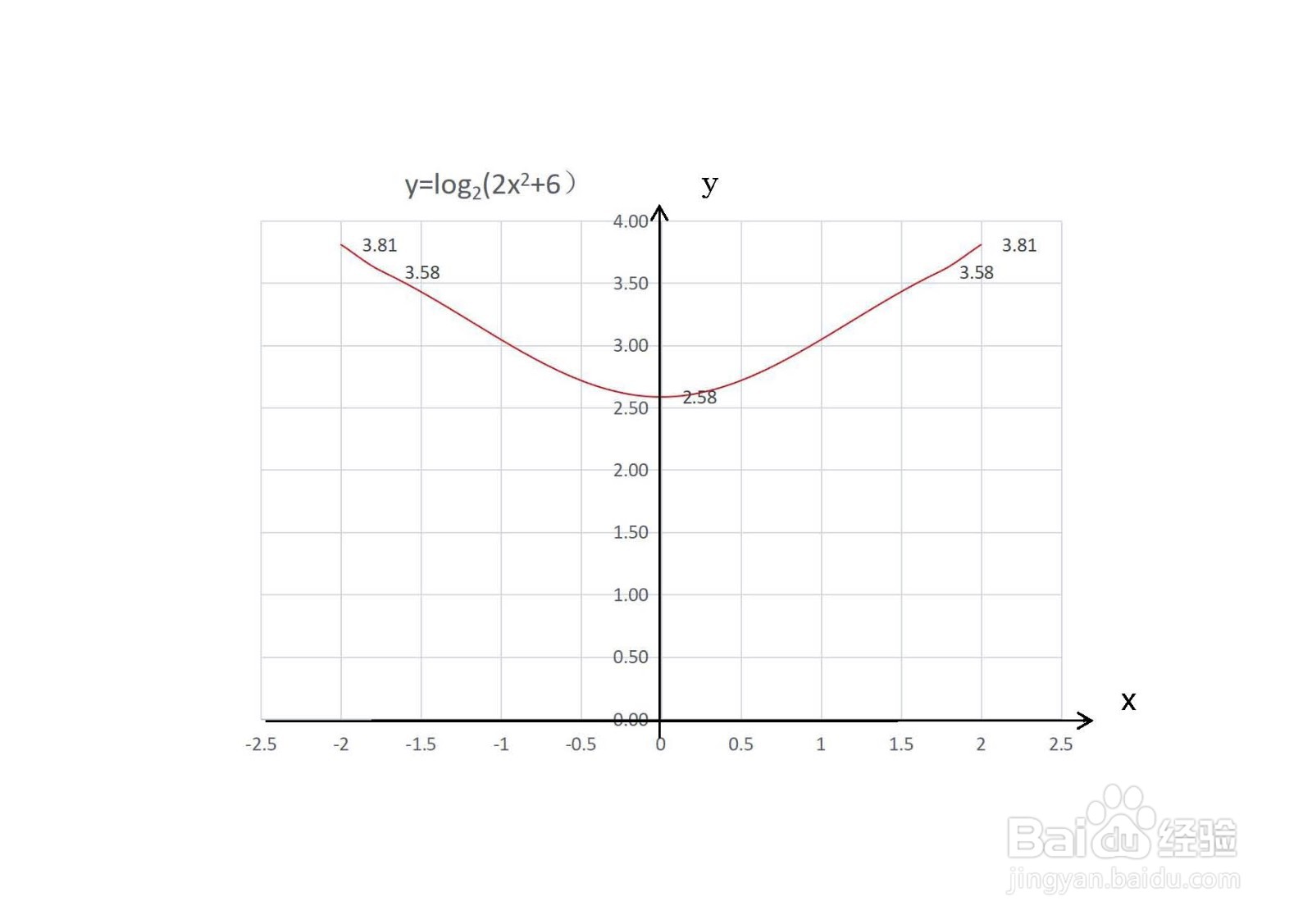
1、结合对数函数的性质,真数大于0,求解函数的定义域。

2、 定义域是指该函数的有效范围,函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合。
3、求解函数的驻点,判断函数的单调性,求出函数的单调区间。
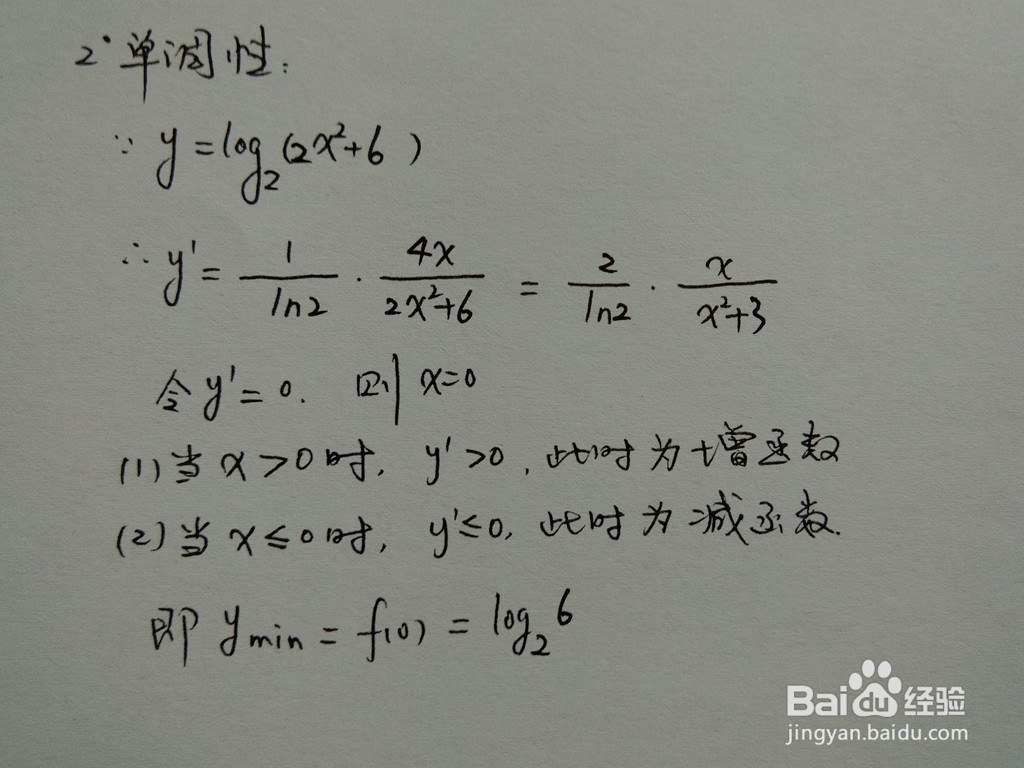
4、函数的单调性是函数的重要性质,反映了随着自变量的增加函数值的变化趋势,它是研究函数性质的有力工具。
5、通过函数的二阶导数,求出函数的拐点,判断函数的凸凹性,进而得到函数的凸凹区间。
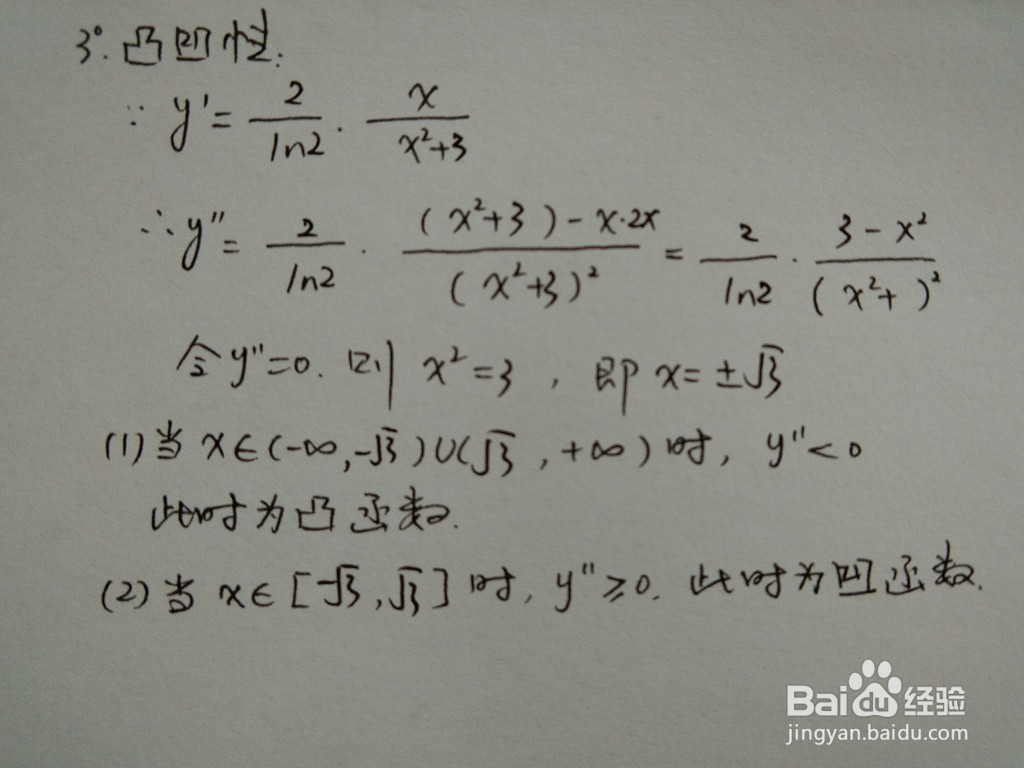
6、 二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数y'=f'(x)仍然是x的函数,则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。
7、判断函数的奇偶性,本函数为偶函数,因为f(-x)=f(x),在全体实数范围内。
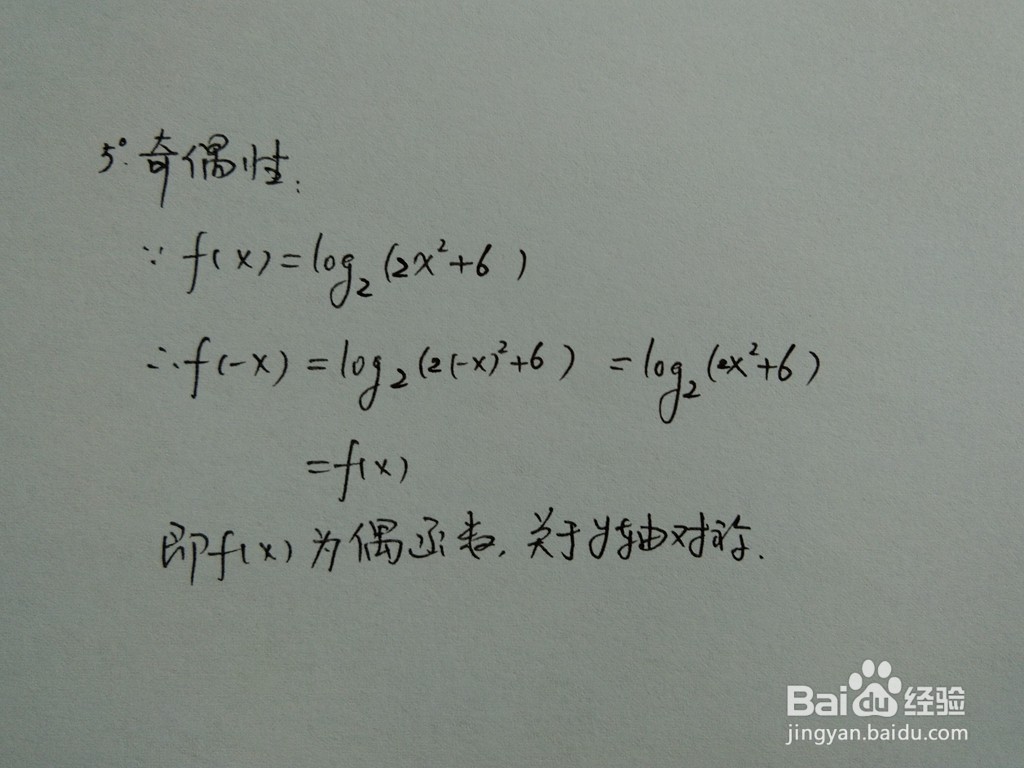
8、函数五点图,函数部分点解析表如下。

9、结合函数的单调性、凸凹性、偶函数等性质,在定义域条件下,即可简要画出函数的示意图如下: