1、通过一阶导数,得函数的驻点,进而判断函数的单调性,求出单调区间。

2、导函数等于零的点称为函数的驻点,在这类点上函数可能会取得极大值或极小值(即极值可疑点)。进一步判断则需要知道导函数在附近的符号。对于满足的一点,如果存在使得在之前区间上都大于等于零,而在之后区间上都小于等于零,那么是一个极大值点,反之则为极小值点。
3、 二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数y'=f'(x)仍然是x的函数,则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。

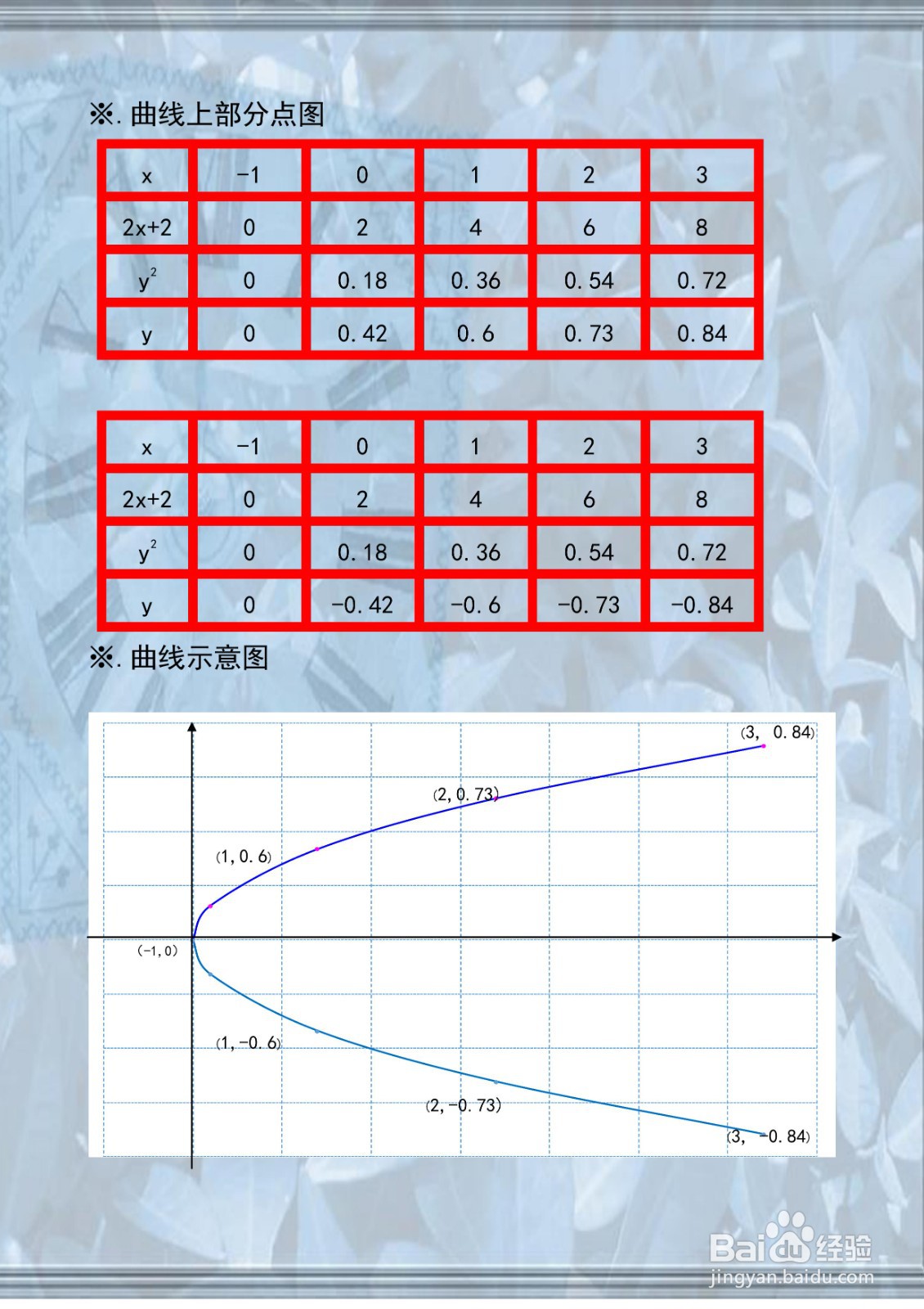
4、函数的五点图表,并画出函数的示意图,综合以上函数的定义域、值域、单调性和凸凹性及极限性质,函数的示意图如下: