1、假设向量u={a巳呀屋饔,b}是标准正交基里面的一个向量,那么:u'.A.u=1这其实是一个不定方程,可以用a表示b:s1=Solve[u.A.u == 1, b]b有两个解,我们可以选择第一个。

2、设v={c,d}是标准正交基里面的另一个向量,同样可以用c表示d:s2 = Solve[v.A.v == 1, d]

3、这样,可以分别写出u和v:u = u /. s1[[1]]v = v /. s2[[1]]

4、u和v关于型正交,就是:u'.A.v=0可以用a把c表示出来:s3 = Solve[u.A.v == 0, c]
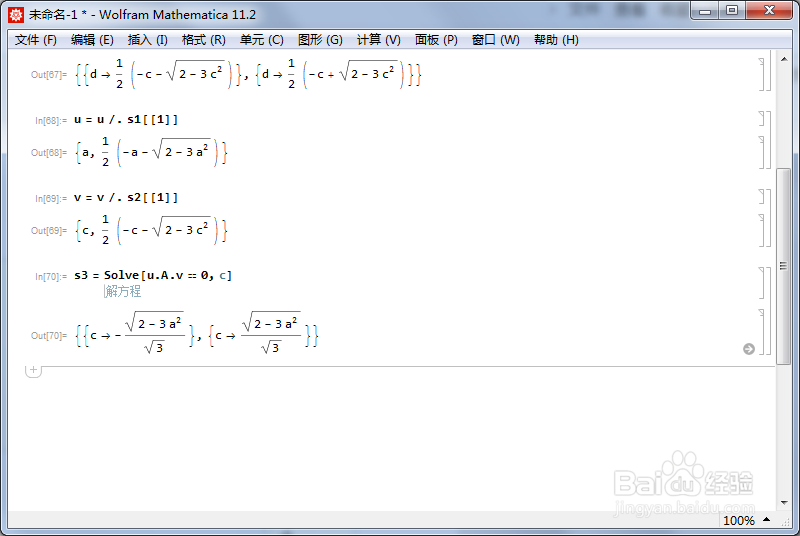
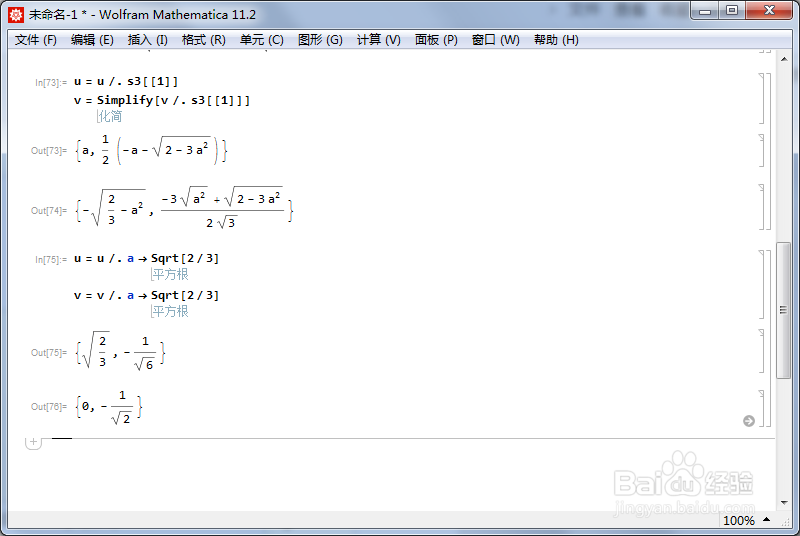
5、重新写u和v:u = u /. s3[[1]]v = Simplify[v /. s3[[1]]]

6、实际上,我们还可以赋予a一个具体的值,比如a->Sqrt职邗珩垃[2/3]:u = u /. a -> Sqrt[2/3]v = v /. a -> Sqrt[2/3]得到的番舸榆毛标准正交基如下。
7、a->0的结果是:u = u /. a -> 0v = v /. a -> 0

