本文,用Mathematica研究一下Mills的相关理论。


工具/原料
电脑
Mathematica
Mills素数
1、Mills常数,指的是,对任意正整数n,A^(3^n)的整数部分都是素数的最小的正实数A,这里,把Mills常数记为θ。在百度百科里,可以查看到,θ的精确值,目前还没办法计算,只知道大体数值θ=1.30637788386308069046...

2、记f[n_] := Floor[θ^3^n],n是正整数,那么称f[n] 为第n个Mills素数。用上面的θ=1.30637788386308069046来算一下,看看前五个数字是不是素数。

3、由上图可知,第四、五个数字不是素数,这说明θ的精度不够,那么怎么才能提高θ的精度呢?这就不得不提一下,于2005 年,数学家Candwell and Cheng提出的一个方法,把θ的数值,精确到小数点后面999位。见下图。a[n_] := {3, 30, 6, 80, 12, 450, 894, 3636, 70756, 97220, 66768}[[n]]f[1] := 2f[n_] := f[n] = f[n - 1]^3 + a[n - 1]

4、用这个θ来看看,能不能得到前五个Mills素数。

5、检测一下,这五个数字,到底是不是素数。

6、那么,第六个Mills素数是多少呢?这个数字很大,而且,越往后,Mills素数越大的离谱。第六个Mills数是84位的素数,而第七个则是253位的素数。
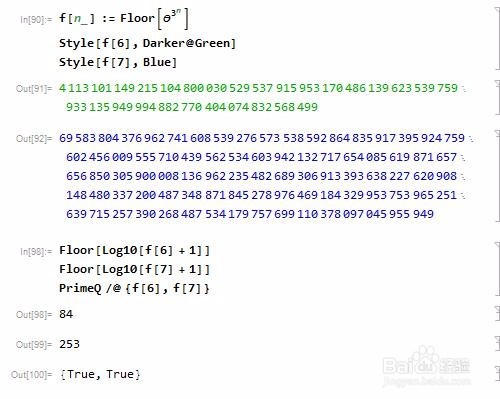
7、我们可以通过数位,来看看Mills素数的增长速度,到底有多快!第20个Mills数的位数,已经超过了四亿位。

