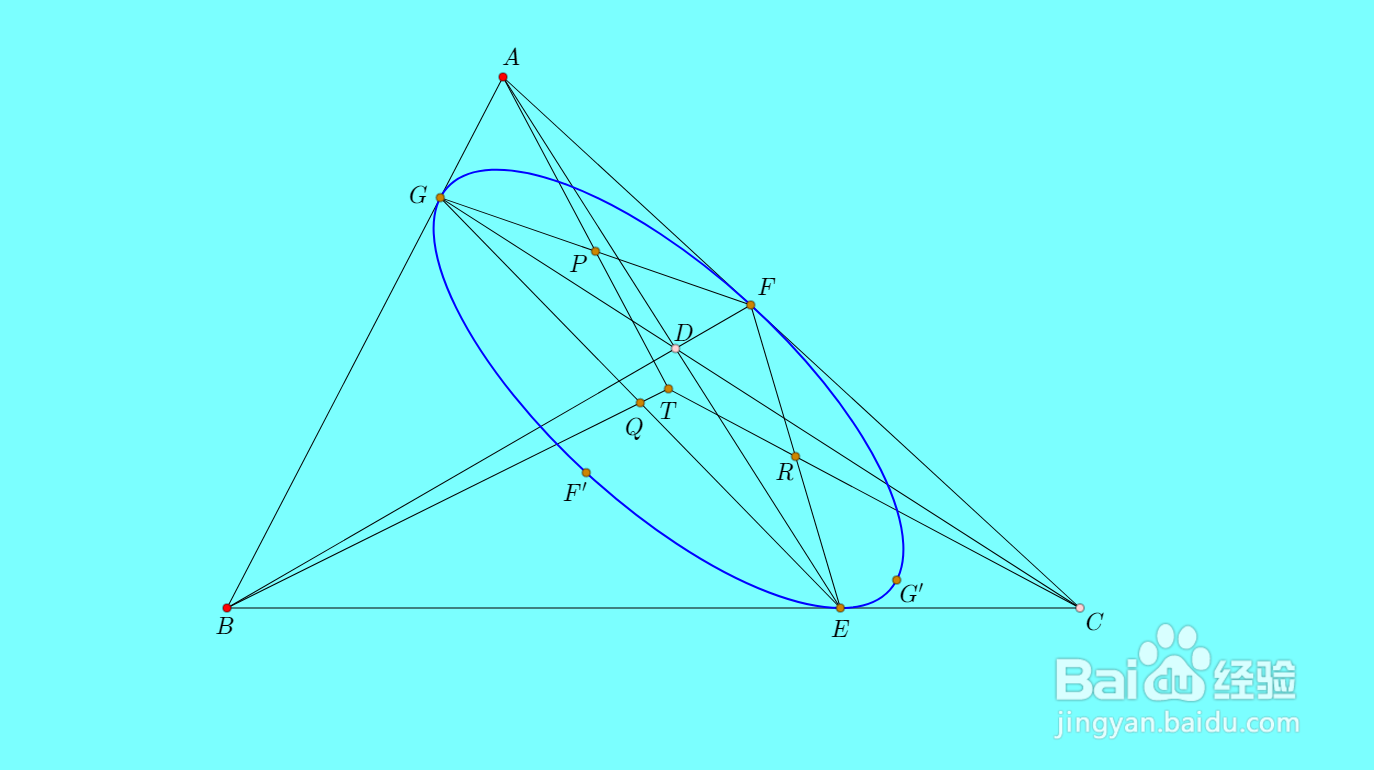
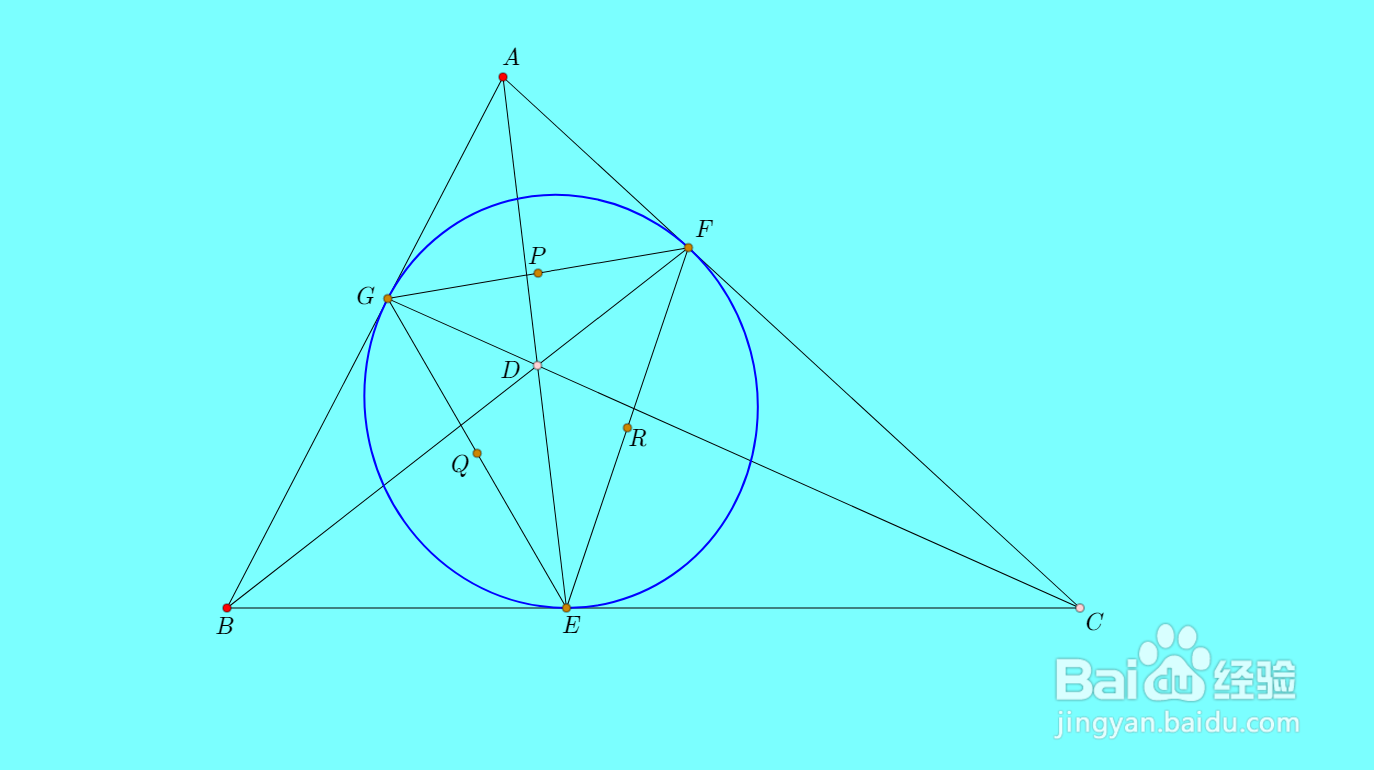
1、如下图,三角形ABC的内切椭圆与三边分别切于E、F、G,则直线AE、BF、CG共点于D。这里,我把D称为这个内切椭圆的塞瓦点,椭圆称为D的塞瓦锥线。D在三角形ABC内部,就一定是内切椭圆。
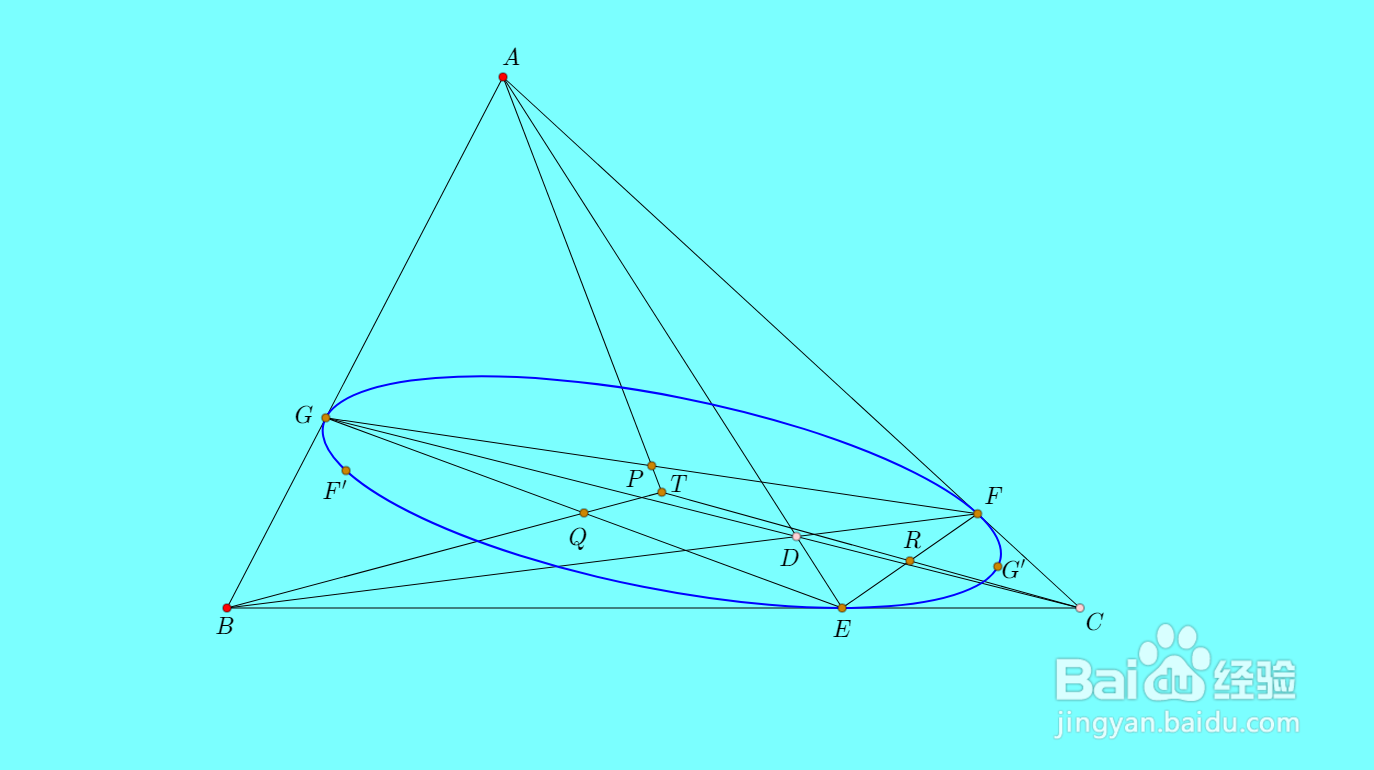
2、如果给定三角形内的点D,如何画出相应的塞瓦锥线呢?首先,E、F、G三点的位置容易确定。
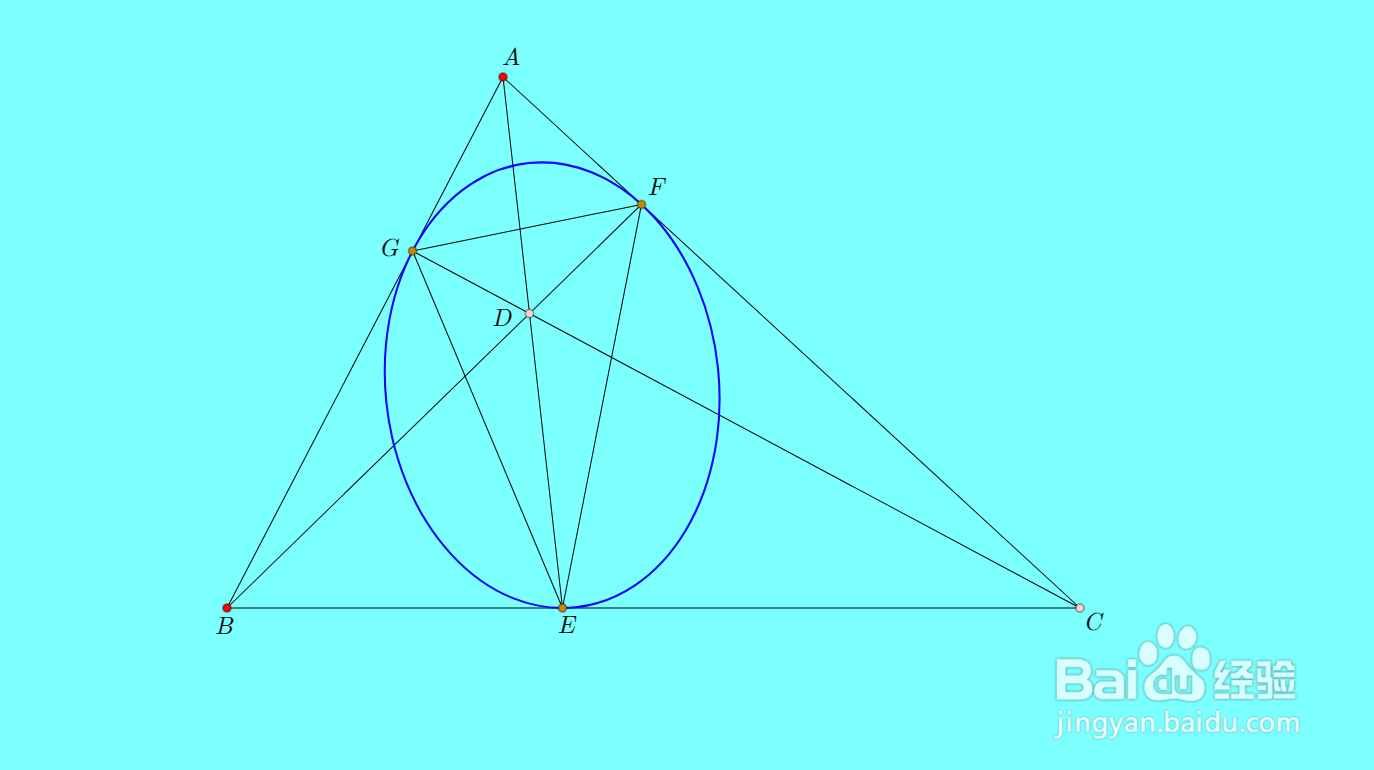
3、取三角形EFG三边中点,分别记为P、Q、R。
4、可以证明,直线AP、BQ、CR共点于T。怎么证明呢?读者可以自己思考一下。
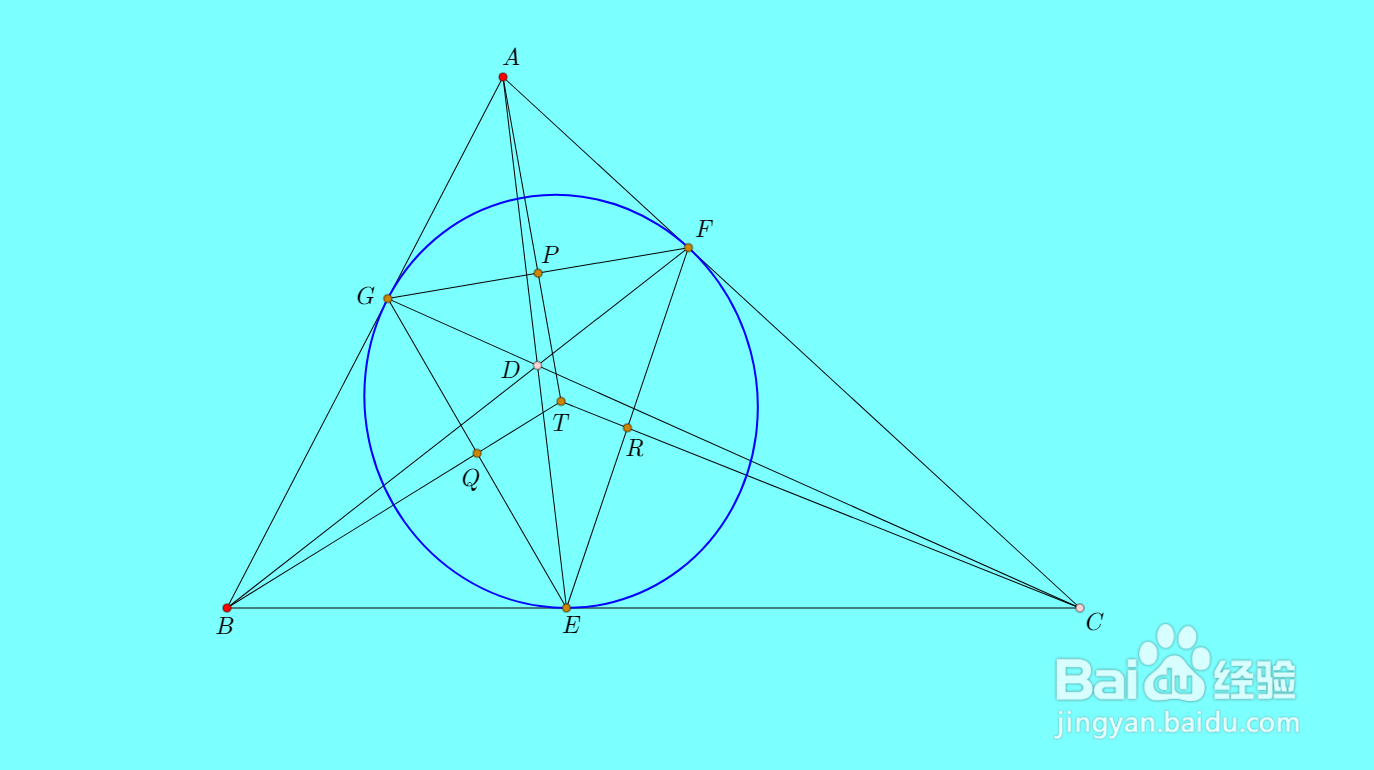
5、根据仿射变换原理,可以证明T就是D的塞瓦锥线的中心点。因此,F和G关于T的对称点F&拭貉强跳#39;和G',也在内切椭圆上。这样,有了五个点E、F、G、F'、G媪青怍牙',就确定了唯一的圆锥曲线。这用网络画板的【过五点的圆锥曲线】工具,就可以实现直接作图。
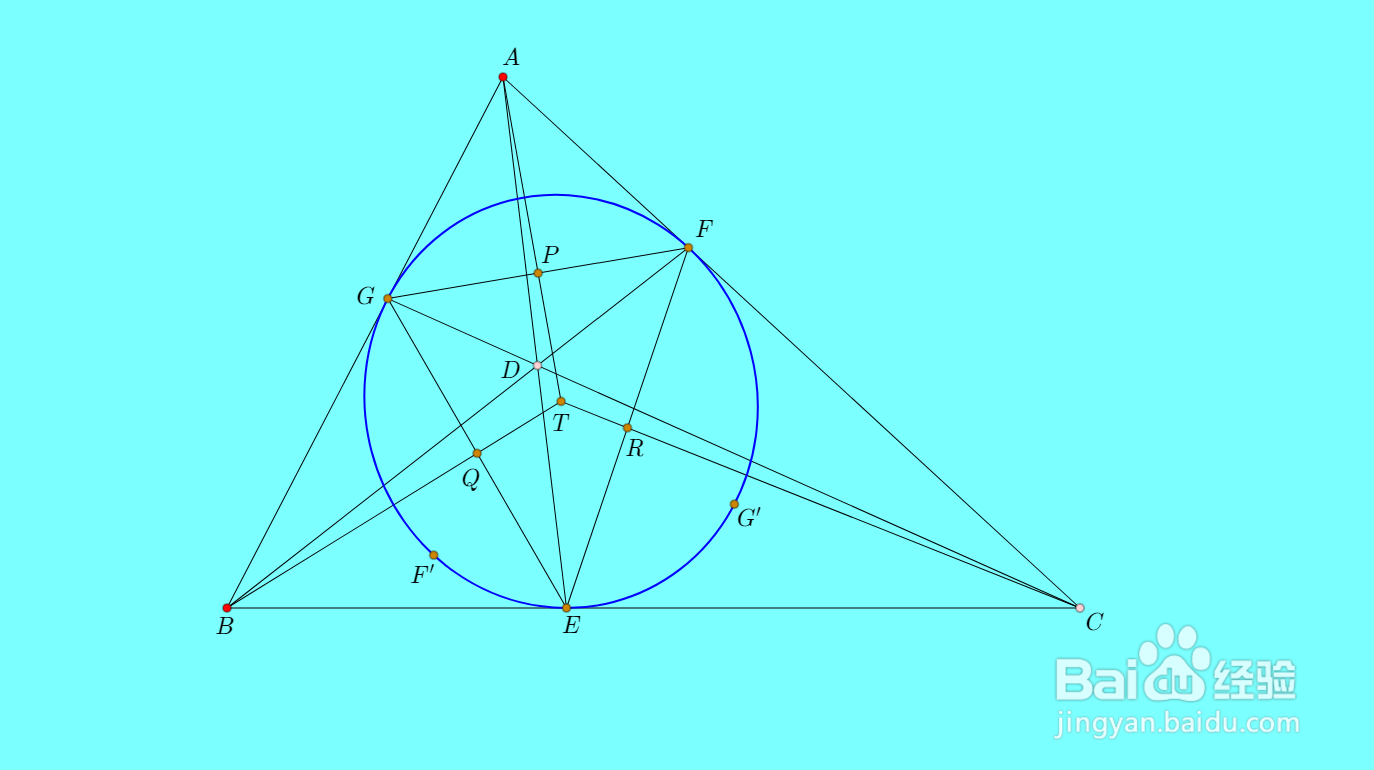
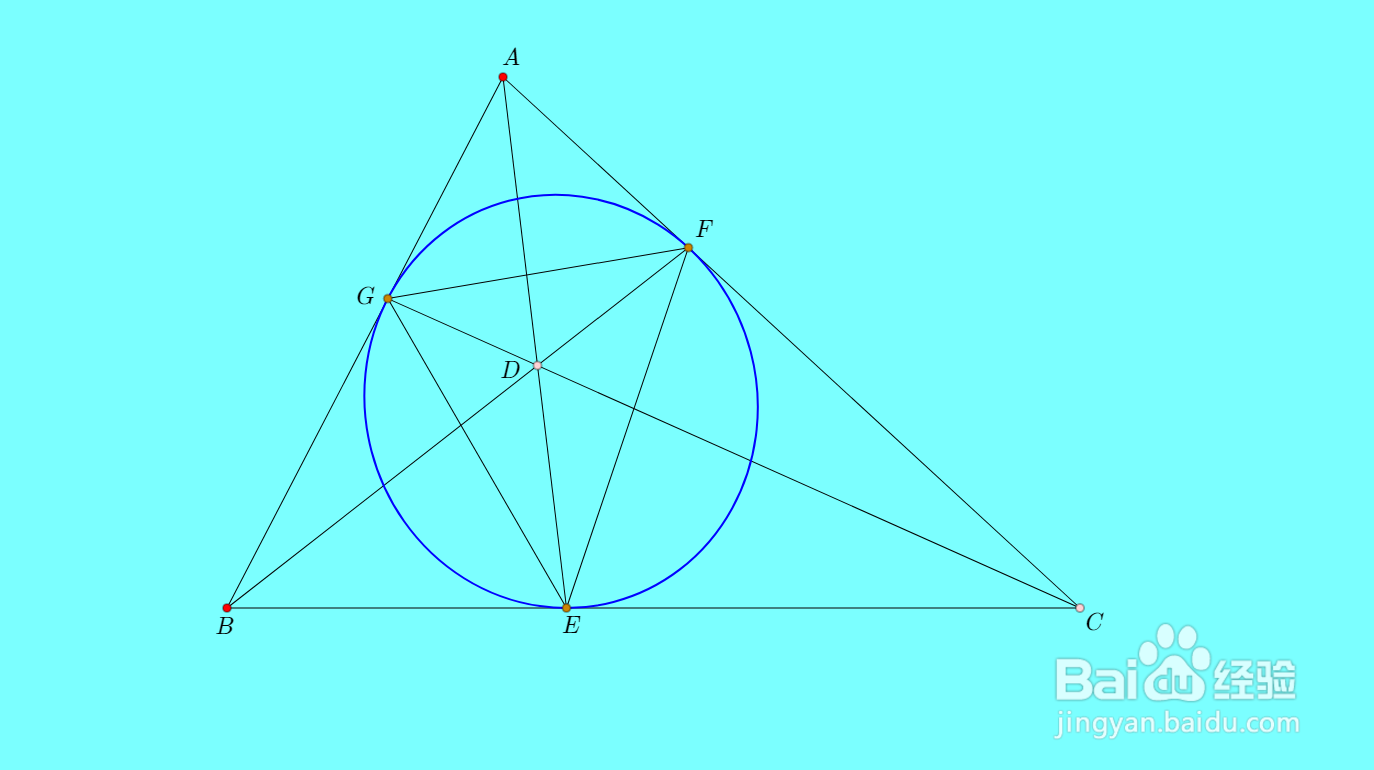
6、随意地拖动D点的位置,可以看到不同形状的内切椭圆。